4.2.1.
Пассивные компоненты
Резисторы
описываются предложением
Rxxx
<+узел> <-узел> [имя модели] <значение>
[ТС=<ТС1>[,<TС2>]]
Здесь
ххх
— произвольная алфавитно-цифровая последовательность общей длиной не более
7 символов, которая пишется слитно с символом R и вместе с ним образует имя
компонента. Например:
R1
1502К
RGEN
1 2 2.4Е4 ТС=0.005
R12
3 О RTEMP 5K
.MODEL
RTEMP RES (R=3 DEV=5%TC1=0.01)
Параметры,
описывающие модель резистора, приведены в табл. 4.14.
Таблица
4.14. Параметры модели резистора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Масштабный множитель
сопротивления
|
|
|
|
|
|
|
Линейный температурный
коэффициент сопротивления
|
|
|
|
|
|
|
Квадратичный
температурный коэффициент сопротивления
|
|
|
|
|
|
|
Экспоненциальный
температурный коэффициент сопротивления
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная
температура
|
|
|
|
|
|
|
Разность между
температурой устройства и модели-прототипа
|
|
|
|
|
|
|
|
|
|
|
Если в описании
резистора
<имя модели>
опущено, то его сопротивление равно параметру
<сопротивление>
в омах. Если
<имя модели>
указано
и в директиве .MODEL отсутствует параметр ТСЕ, то сопротивление резистора определяется
выражением
<значение>-&
[
1+ТС1 (T-Tnom)+TC2(T-Tnom)
2
];
Если параметр
ТСЕ указан, то сопротивление равно <значение>R*1,01
ТСЕ(т
"
Тпоm)
Здесь Т —
текущее значение температуры (указывается по директиве .TEMP); Tnom= 27 °С
— номинальная температура (указывается по директиве .OPTIONS).
Параметр
<значение>
может быть как положительным, так и отрицательным, но не равным нулю.
Спектральная
плотность теплового тока резистора рассчитывается по формуле Найквиста
S
i
(f)=4kT/<сопротивление>.
Для резисторов с отрицательным сопротивлением в этой формуле берется абсолютное
значение сопротивления.
Направление
падения напряжения на резисторе (как и на произвольном двухполюсном компоненте)
и тока через него указаны на рис. 4.8, а.
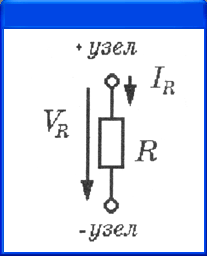
а)

б)
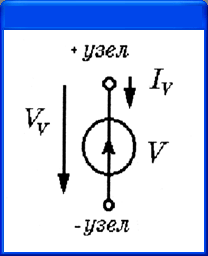
в)
Рис. 4.8.
Типовые двухполюсники: а — резистор; б — источник тока; в — источник напряжения
Конденсатор
описывается предложением
Сххх
<+узел> <-узел> [имя модели] <значение> +
[IС=<
начальное
значение напряжения>]
Например:
С1
15056pF
C2390.5pFIC=1.5V
C346CMOD10uF
.MODEL
CMOD CAP(C=2.5 TC1=0.01 VC1=0.2)
Параметры
модели конденсатора приведены в табл.4.15.
Таблица
4.15. Параметры модели конденсатора
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Масштабный множитель
емкости
|
|
|
|
|
|
|
Линейный коэффициент
напряжения
|
|
|
|
|
|
|
Квадратичный
коэффициент напряжения
|
|
|
|
|
|
|
Линейный температурный
коэффициент емкости
|
|
|
|
|
|
|
Квадратичный
температурный коэффициент емкости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная
температура
|
|
|
|
|
|
|
Разность между
температурой устройства и модели-прототипа
|
|
|
|
|
|
|
|
|
|
|
Если в описании
конденсатора
<имя модели>
опущено, то его емкость равна параметру
<значение>
в фарадах, в противном случае она определяется выражением
<значение>-С(1+VVСV+VС2.V
2
)[1+ТС1(Т-Тпоm)
+ TC2(T-Tnom)
2
].
Здесь V —
напряжение на конденсаторе при расчете переходных процессов (режим TRAN). При
расчете частотных характеристик (режим АС) емкость считается постоянной величиной,
определяемой в рабочей точке по постоянному току.
После ключевого
слова IC указывается значение напряжения на конденсаторе при расчете режима
по постоянному току, которое при расчете переходных процессов служит начальным
значением этого напряжения.
Индуктивность
описывается предложением
Lxxx<+yзел>
<-узел> [имя модели] <значение> +
[IС=<
начальное значение
тока>]
Например:
L1
15020mH
L2
1 2 0.2Е-6
L3
4 6 2VH Ю=2
LOAD
5 12 LMOD 0.03
.MODEL
LMOD IND (L=2 DEV=20% IL1=0.1)
Параметры
модели индуктивности приведены в табл. 4.16.
Таблица
4.16. Параметры модели индуктивности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Масштабный множитель
индуктивности
|
|
|
|
|
|
|
Линейный коэффициент
тока
|
|
|
|
|
|
|
Квадратичный
коэффициент тока
|
|
|
|
|
|
|
Линейный температурный
коэффициент индуктивности
|
|
|
|
|
|
|
Квадратичный
температурный коэффициент индуктивности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Относительная
температура
|
|
|
|
|
|
|
Разность между
температурой устройства и модели-прототипа
|
|
|
|
|
|
|
|
|
|
|
Если в описании
опущено
<имя модели>,
то индуктивность равна параметру
<значение>
в генри, в противном случае она определяется выражением
<значение>-
L(
1+IL1.1+IL2.I
2
)[ I+TC1 (T-Tnom)+TC2(T-Tnom)
2
].
Здесь I —
ток через катушку индуктивности при расчете переходных процессов (режим TRAN).
При расчете частотных характеристик (режим АС) индуктивность считается постоянной
величиной, определяемой в рабочей точке по постоянному току.
После ключевого
слова IC указывается значение тока через катушку индук-тивностей при расчете
режима по постоянному току, которое при расчете переходных процессов служит
начальным значением этого тока.
Взаимная
индуктивность
описывается следующим предложением
Кххх
Lyyy Lzzz... <коэффициент связи>
Порядок перечисления
имен индуктивностей
Lyyy, Lzzz, ...
безразличен, знак взаимной индуктивности
определяется порядком перечисления узлов в описании каждой индуктивности. Параметром
взаимной индуктивности является
<коэффициент связи>.
Если в трансформаторе
имеется несколько обмоток, то можно либо определить взаимные индуктивности для
каждой попарной комбинации обмоток в отдельных предложениях, либо в одном предложении
указать список всех индуктивностей, имеющих одинаковый коэффициент связи. Например,
трехобмоточный высокочастотный трансформатор (рис. 4.9) описывается следующим
образом:
I1
1 0АС1МА L1 1 010UH L22310UH L33410UH K12L1 L2L30.8
Здесь I1 —
источник тока, комплексная амплитуда которого в режиме АС имеет значение 1 мА.
Первый узел в описаниях индуктивностей LI, L2, L3 обозначает начало обмотки.

Рис. 4.9.
Трехобмоточный трансформатор
Коэффициент
связи двух обмоток определяется выражением
коэффициент
связи = Mij/ (корень LiLj)
где
Li
Lj
— индуктивности обмоток;
M
tj
— их взаимная индуктивность.
Напряжение
на катушке
L
i
с учетом взаимной индукции определяется выражением
Vi = Li
*dl
i
/dt+ Мij*dl
i
/dt + М
ik
*dl
k
/dt+...
Магнитный сердечник трансформатора
описывается предложением
KxxX Lyyy
Lzzz ... <коэффициент связи> <имя модели>
+
[<масштабный
коэффициент>]
На одном сердечнике
помещается одна или несколько обмоток с именами
Lyyy, Lzzz, ...
Все обмотки
имеют одинаковый
<коэффициент связи>.
При описании каждой обмотки
Lyyy,
упомянутой в составе сердечника, изменяется смысл параметра
<значение>
— теперь он определяет не индуктивность, а число витков обмотки сердечника.
Например, трансформатор с пермаллоевым сердечником МП60 (рис. 4.10) описывается
предложениями:
OL1
15 1050; 50 витков
L2
10 0 150; 150 витков
K2L1
L20.99TI125V
.MODEL
T1125V CORE (LEVEL=2 MS=334E3 ALPHA=2.5E-2 A=4.05E3 K=166 C=0.05
+
AREA=0.064 PATH=2.25)
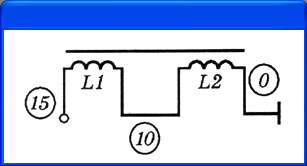
Рис. 4.10.
Трансформатор с магнитным сердечником
Параметр
<масштабный
коэффициент>
изменяет площадь поперечного сечения магнитопровода (по
умолчанию равен единице). Она равна произведению этого коэффициента на параметр
модели сердечника AREA.
График кривой
намагниченности сердечника выводится на экран (в программе Probe, см. разд.
5.1) при наличии директивы .PROBE; с помощью директив .PRINT и .PLOT эти данные
не выводятся.
В программе
PSpice используется
модель магнитного сердечника,
предложенная Джилсом
и Атертоном [7]. Она основана на известных представлениях о движении доменных
границ магнитных материалов. С ее помощью удается отразить все основные характеристики
гистерезиса, такие, как кривая начальной намагниченности, намагниченность насыщения,
коэрцитивная сила, остаточная намагниченность и динамические потери на гистерезис.
Существуют
две разновидности этой модели — LEVEL = 1 и LEVEL = 2, из которых модель LEVEL
= 1 оказалась неудачной и ее исключили из PSpice 8.0. Параметры модели LEVEL
= 2 приведены в табл. 4.12.
Таблица
4.17. Параметры модели магнитного сердечника
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр формы
безгистерезисной кривой намагничивания
|
|
|
|
|
|
|
Площадь поперечного
сечения маг-нитопровода
|
|
|
|
|
|
|
Постоянная упругого
смещения доменных границ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Постоянная подвижности
доменов
|
|
|
|
|
|
|
Намагниченность
насыщения
|
|
|
|
|
|
|
Коэффициент заполнения
сердечника
|
|
|
|
|
|
|
Средняя длина
магнитной силовой линии
|
|
|
|
|
|
|
|
|
|
|
Параметры
AREA, PATH, GAP
и
PACK
определяются геометрическими размерами
сердечника, остальные — свойствами магнитного материала.
Линия передачи
описывается двояко.
Линия передачи без потерь
описывается предложением
Тххх
<+узел порта А> <—узел порта А> <+узел порта В>
+
<-узел порта В> [имя модели]
+
ZО=<значение>
[ТD=<значение>]
+
[F=<значение> [NL=<значение>]]
+
I
С=<
напряжение на входе А> <ток входа А>
+
<напряжение на входе В> <ток входа В>
Здесь ZO —
волновое сопротивление линии (Ом); TD — задержка сигнала в линии (с); NL — электрическая
длина линии на частоте F (NL = 1/л, где 1 — геометрическая длина линии, л, —
длина волны в линии, по умолчанию NL = 0,25).
Примечание.
Одинаково воспринимаются
ZO (буква «О») и ZO (цифра «О»). При описании линии
передачи задается параметр TD либо F и NL. Например
Т1
1 2 3 4 ZO50
Т2
1 2 3 4 ZO=75 TD=115ns
ТЗ
1 2 3 4 ZO=75 F=4.5MEG
T4
1 2 3 4 ZO=75 F=4.5MEG NL=0.5
С помощью
ключевого слова IC задаются начальные значения напряжений и токов на выводах
линии передачи. Схема замещения линии передачи без потерь при расчете переходных
процессов или режима по постоянному току изображена на рис. 4.21,
а.
При
расчете частотных характеристик эта линия представляет собой безынерционное
звено.
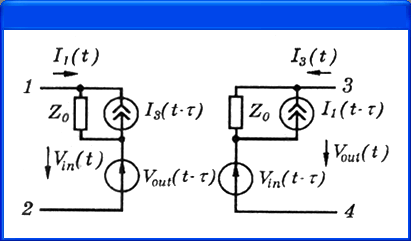
а)
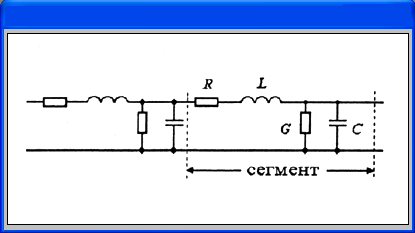
б)
Рис. 4.11.
Модель линии передачи без потерь (а) и с их учетом (б)
Линия передач
с потерями
описывается предложением (рис. 4.11, б):
Тххх <+узел
порта А> <-узел порта А> <+узел порта В> <-узел порта В>
+ [<имя модели> [электрическая длина]] LEN=<значенue> + R=<значение>
L=<значение> С=<значение> С=<значение>
Здесь LEN
— длина линии (м); R, L, G, С — погонные сопротивление линии (Ом/м), индуктивность
(Гн/м), проводимость (См/м), емкость (Ф/м).
В принципе
длину линии можно указывать в любых единицах, например в километрах, но тогда
нужно соответствующим образом пересчитать значения погонных параметров R, L,
G и С.
По этим данным
аналитически рассчитывается комплексный коэффициент передачи линии. Анализ переходных
процессов производится с помощью интеграла свертки с импульсной характеристикой
линии, которая вычисляется как преобразование Фурье коэффициента передачи.
Модель линии
передачи описывается предложением:
.MODEL
<имя
модели>
TRN
(параметры модели)
Она характеризуется
параметрами, указанными в табл. 4.18.
Таблица
4.18. Параметры модели линии задержки
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Идеальная линия
без потерь
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электрическая
длина на частоте F
|
|
|
|
|
|
|
Начальные значения
напряжений и токов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечания.
1. Модель линии передачи
с потерями требует больших затрат времени при моделировании и не обеспечивает
высокую точность расчетов. Поэтому иногда приходится самостоятельно составлять
их цепочечные схемы замещения, показанные на рис. 4.11, б (обратим внимание,
что в программе PSpice используется другая, встроенная аналитическая модель
линии передачи с потерями, требующая больших вычислительных затрат).
2. В представленных моделях
можно учесть частотные зависимости погонных параметров R, L и G, существенные
при моделировании реальных протяженных линий передачи. Для этого необходимо
задать выражения для параметров R(s) и G(s) как функции комплексной переменной
s — таким образом имитируется частотная зависимость поверхностного эффекта
и потерь в диэлектрике.
3. Линия передачи с потерями
при R = G = 0 и LEN = 1 м эквивалентна идеальной линии с волновым сопротивлением
ZO = -\JL/C и временем задержки TD = LEN корень( L-C.)
Связанные
линии передачи
описываются предложением
Кххх 1<имя
1-й линии передачи> 1<имя 2-й линии передачи> + Ст=<взаимная емкость>
[Lт-<взаимная индуктивность>
Здесь Cm,
Ф/м, и Lm, Гн/м — взаимные емкости и индуктивности связанных линий. Эти параметры
представляют собой недиагональные элементы симметричных матриц взаимных емкостей
и индуктивностей
|
|
|
|
|
C11
|
C12
|
|
|
|
|C|
|
=
|
|
|
|
|
|
|
|
|
|
|
|
C21
|
C22
|
|
|
где
С
12
= C
21
=
—Cm, L
12
= L
21
= - Lm.
Диагональные
элементы матрицы взаимных емкостей равны
C
ii
=C
ig
+Сумма|C
ii
,|,
где
C
ig
— погонная емкость i-й линии передачи. Элементы L
11
, L
22
— погонные индуктивности первой и второй линий передач соответственно. Пусть
имеются две связанные линии передачи, задаваемые соотношениями
Т1
1 0 2 О R=.31 L=.38u G=6.3u C=70p LEN=1 Т2 3 0 4 О R=.29 L=.33u G=6.0u C=65p
LEN=1 К12Т1 Т2 Lm=.04u Cm=6p
Тогда для
их моделирования составляются матрицы взаимных емкостей и индуктивностей следующего
вида:
|
|
|
|
|
75p
|
-6p
|
|
|
|
|C|
|
=
|
|
|
|
|
|
|
|
|
|
|
|
-6p
|
71p
|
|
|
|
|
|
|
|
0.38u
|
0.04u
|
|
|
|
|L|
|
=
|
|
|
|
|
|
|
|
|
|
|
|
0.04u
|
0.33u
|
|
|
Применяемый
в программе PSpice метод моделирования связанных линий является приближенным
и обеспечивает удовлетворительные результаты для линий с малыми потерями.



