4.2.5.
Аналоговые функциональные блоки
Аналоговые
функциональные блоки моделируются с помощью источников напряжения (Е) или тока
(G). В отличие от рассмотренных выше зависимых источников здесь разрешается
использовать параметры и любые функции от узловых потенциалов, токов (через
независимые источники напряжения) и времени.
Нелинейные
передаточные функции
задаются по формату
Еххх <+узел>
<-узел> VALUE
={<выражение>}
Gххх<+узел>
<-узел>
VALUE
={<выражение>}
После ключевого
слова VALUE в фигурных скобках приводится алгебраическое выражение, зависящее
от узловых потенциалов, разности узловых потенциалов, токов через независимые
источники напряжения и времени, например
ESIGNAL
2 0 VALUE={50mV* SIN(6.28*100kHz*TIME)*V(3,4)} GPW 6 О VALUE={V(5)*I(VP)}
Здесь для
текущего времени выделено ключевое слово TIME. .
Область управляемых
источников с нелинейным законом управления очень обширна. В частности, нелинейные
проводимости или резисторы имитируются в программе PSpice с помощью источников
напряжения, управляемых собственным током, или источников тока, управляемых
собственным напряжением. Пример имитации
нелинейного резистора
дан на
рис. 4.20; его описание имеет вид
G
1 2 VALUE={F(V(G))}
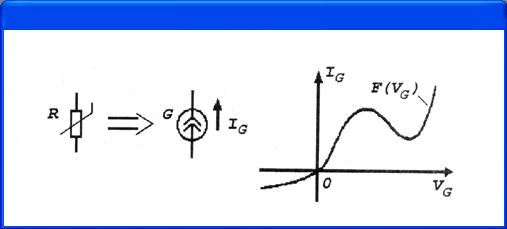
Рис. 4.20.
Имитация нелинейного резистора с помощью источника тока, управляемого собственным
напряжением
Нелинейная
функция F(V(G)), описывающая нелинейную зависимость тока от падения напряжения
на резисторе, должна быть определена в задании на моделирование до строки с
описанием источника G, например
.FUNC
F(X)=1e-6*(1-EXP(-40*X))
Замечание.
В режимах .TRAN и .DC
значения источников Exxx, Ixxx вычисляются согласно приведенным в фигурных
скобках выражениям. Если это выражение представляет собой линейную функцию
нескольких переменных, то в режиме .АС данный источник представляет собой
линейный управляемый источник. При этом, если в выражение входит переменная
TIME, она полагается равной нулю. Если же это выражение представляет собой
нелинейную функцию одной переменной, то после расчета режима цепи по постоянному
току выражение в фигурных скобках линеаризуется и в частотной области такой
источник представляет собой линеаризированный управляемый источник. Нелинейную
функцию нескольких переменных при расчете частотных характеристик использовать
нельзя - результаты будут непредсказуемы. Эти же замечания справедливы и для
описываемого ниже табличного задания управляемых источников.
Табличное
описание
передаточной функции вводится по формату
Еххх <+узел>
<-узел> TABLE
{<выражение>} «аргумент> <функция>>*
Gxxx <+узел>
<-узел> TABLE
{<выражение>} «аргумент> <фунщия>>*
Входом таблицы
является
<выражение>,
которое содержит любую комбинацию напряжений
и токов. При обращении к управляемому источнику вычисляется значение выражения
и берется значение функции из таблицы с помощью линейной интерполяции между
опорными точками, задаваемыми парами чисел
(<аргумент>, <функция>).
Например, ВАХ туннельного диода, рассматриваемого как нелинейная проводимость
(рис. 4.30), может быть задана в виде
GR
1 2TABLE{V(GR)}=(0.0)(.01.1mA)
+
(.02,1.1mA) (0.05,2mA) (.06,3mA) (.065,3.2mA) (.8,1.5mA) (1,3mA) (1.5,5mA)
Координаты
опорных точек задаются в порядке возрастания аргумента.
Заметим, что
отсутствие аппроксимации табличных значений сплайнами более высоких порядков,
чем линейная интерполяция, в ряде случаев приводит к слишком большим ошибкам.
Линейные
функциональные блоки
моделируются в терминах соотношения между выходными
и входными переменными в частотной области. По директиве .АС определяются значения
комплексного коэффициента передачи блока на каждой частоте. При расчете рабочей
точки по постоянному току и по директиве .DC берется значение коэффициента передачи
на нулевой частоте (поэтому изображения по Лапласу всех узловых потенциалов
не должны иметь составляющих типа 1/s). По директиве .TRAN выходная переменная
блока вычисляется как интеграл Дюамеля (свертка входного воздействия с импульсной
характеристикой блока), что значительно увеличивает длительность расчетов. Возможны
следующие варианты задания линейных блоков.
Передаточная
функция управляемого источника задается с помощью
преобразования Лапласа:
Еххх <+узел>
<-узел>
LAPLACE
{<выражение>}= + {<передаточная функция
в s-области>}
Gxxx <+узел>
<-узел>
LAPLACE
{<выражение>}= + {<передаточная функция
в s-области>}
Например,
передаточная функция активного RC-фильтра задается следующим образом:
EARC 2 О LAPLACE
{V(9)}={5/(H-0.01*s)}
Фильтр
с чебышевской передаточной функцией
задается в виде
Еххх <+узел>
<-узел>
CHEBYSHEV
{<выражение>}=<тип> + <граничная
частота>* <затухание>*
Gxxx <+узел>
<-узел>
CHEBYSHEV
{<выражение>}=<тип> + <граничная
частота>* <затухание>*
Здесь
<тип>
- тип фильтра, принимающий значения: LP - фильтр нижних частот, HP - фильтр
верхних частот, ВР - полосовой фильтр, BR - режекторный фильтр.
Для задания
желаемой характеристики фильтра задается список граничных частот (для ФНЧ и
ФВЧ задаются две частоты, для ПФ и РФ - четыре) и затем список затуханий на
этих частотах в децибелах; порядок следования граничных частот безразличен.
Приведем примеры:
Е1
3 4 CHEBYSHEV {V(10)}=LP 800 1.2К 0.10В 50dB
Е2
5 6 CHEBYSHEV {V(10)}=BP 800 1.2К 2К ЗК 0.1dB 50dB
Табличное
описание
комплексной передаточной функции в частотной области задается по
формату
Еххх <+узел>
<-узел>
FREQ
{<выражение>}=[KEYWORD] + <<частота>,<модуль>,<фаза>>*
[DELAY]=<задержка>]
Сххх<+узел>
<-узел>
FREQ {<выражение>}=[
KEYWORD
] + <<
частота>,<модуль>,<фаза>>*
[DELAY]=<задержка>]
Здесь частота
задается в герцах, модуль передаточной функции - в децибелах, фаза передаточной
функции - в градусах. Значения опорных точек указываются в порядке возрастания
частоты. Максимальное количество точек - 2048. Например, передаточная функция
типа фильтра верхних частот задается так:
EHIGHPASS
2 О FREQ (V(9)} (0,-60,69.1) (2kHz,-3,45) (5kHz,0,0)
С помощью
ключевого слова KEYWORD изменяется способ задания таблицы передаточной функции.
Оно может принимать следующие значения:
-
MAG - задание абсолютных
значений передаточной функции вместо децибел;
-
DB - задание значений
передаточной функции в децибелах (принимается по умолчанию);
-
RAD - задание фазы
в радианах;
-
DEG - задание фазы
в градусах (принимается по умолчанию);
-
R_I - задание действительной
и мнимой части передаточной функции вместо ее модуля и фазы.
Ключевое слово
DELAY задает дополнительную задержку, которая принимается во внимание при расчете
фазовой характеристики фильтра.
В качестве
еще одного примера составим структурную схему моделирования рассмотренной выше
системы дифференциальных уравнений:
dx
1
/dt
= -0,3x
1
+
х
2
+ х
1
2
- 3x
1
x
2
-
x
1
,
dx
2
/dt
= 0,24 - 0,6x
2
+
4х
1
х
2
- 6х
1
2
х
2
с помощью
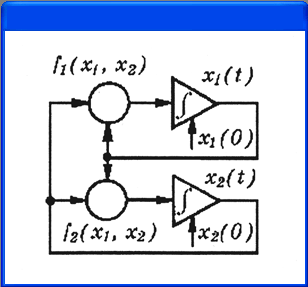
интеграторов. На рис. 4.31,
а
представлена функциональная схема моделирования
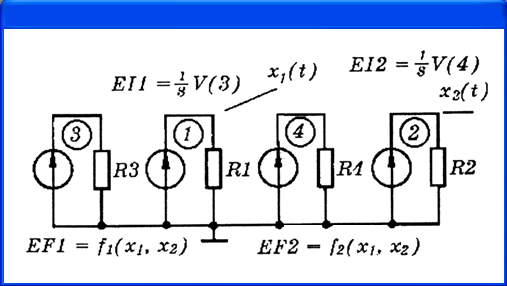
этой системы уравнений, а на рис. 4.31, б - ее реализация в компонентном базисе
программы PSpice. В ней использованы управляющие источники напряжения E11, EI2
,
заданные с помощью преобразования Лапласа и выполняющие операции интегрирования,
а также нелинейные управляемые источники напряжения
EF1, EF2
для вычисления
правых частей системы уравнений. На входном языке программы PSpice задание на
решение рассматриваемой системы уравнений имеет вид:
Laplace
transforms
EM
1 0 LAPLACE {V(3)}={1/s}
EI2
2 0 LAPLACE {V(4)}={1/s}
EF1
3 0 POLY(3) (1,0) (2,0) (0,0) 0-0.3101-300001
EF2
4 0 POLY(3) (1,0) (2,0) (0,0) 0.6 0 -0.6 00400000-6
R1
1 01E9
R2201E9
R3301E9
R4401E9
.ICV(1)=0V(2)=0.4
.TRAN
0.1s 40s SKIPBP
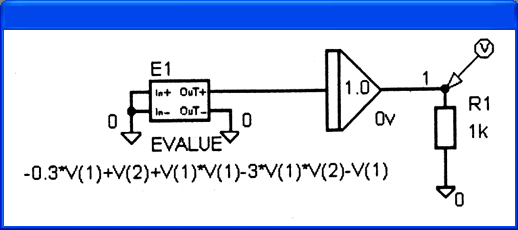
На рис. 4.31,
в
показана реализация этой же схемы с помощью графического редактора
PSpice Schematics. В ней использованы символы интеграторов INTEG и управляемых
источников напряжения EVALUE из библиотеки символов amb.slb (см. Приложение
2 [7]). Резисторы
R1, R2
на этой схеме необходимы только для соблюдения
правил составления топологии схемы, согласно которым к выходным зажимам компонентов
- в данном случае интеграторов - должна быть подключена нагрузка. Если это неудобно,
то нужно отредактировать символ INTEGER, изменив атрибуты вывода Out (выход),
изменив в разделе
If unconnected
(если вывод не подсоединен) значение
параметра Float=UniqueNet - создать узел для подключения маркера. После этого
резисторы
Rl, R2
можно из схемы на рис. 4.21,
в
удалить.
а)
б)
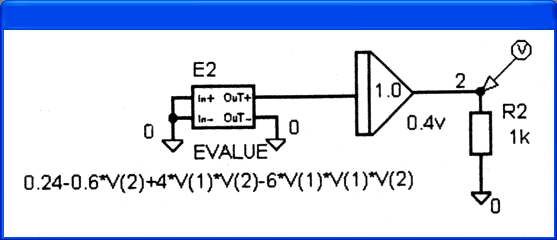
в)
Рис. 4.21.
Функциональная схема моделирования системы двух дифференциальных уравнений {а),
ее реализация в виде принципиальной схемы, созданной вручную (б) и с помощью
PSpice Schematics (в)



